 暂无AI摘要
暂无AI摘要
一、实验概述
实验需要使用Python语言和鸢尾花(Iris)数据集。需要利用scikit-learn库来加载数据集并将其分为训练集和测试集,然后实现kNN算法。最后我们可以通过交叉验证来评估kNN算法的性能,并且利用matplotlib等绘图库对实验结果可视化。
实验环境
windows11、Python3.9、pycharm
二、实现kNN算法并使用鸢尾花数据集测试
(1)代码实现
# 导入所需库
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, KFold
from collections import Counter
# 定义欧氏距离计算函数
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
# 定义 KNN 算法函数
def knn(X_train, y_train, X_test, k):
y_pred = [] # 初始化预测结果列表
for test_point in X_test:
distances = [] # 存储测试点到所有训练点的距离及其对应的标签
for train_point, label in zip(X_train, y_train):
dist = euclidean_distance(test_point, train_point) # 计算距离
distances.append((dist, label)) # 将距离和对应的标签添加到列表中
distances.sort(key=lambda x: x[0]) # 按距离升序排列
k_nearest_neighbors = [label for _, label in distances[:k]] # 获取前 k 个最近邻的标签
most_common = Counter(k_nearest_neighbors).most_common(1) # 找到出现次数最多的标签
y_pred.append(most_common[0][0]) # 添加到预测结果列表中
return y_pred
# 定义交叉验证函数
def cross_val_knn(X, y, k, n_splits):
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=42) # 定义 KFold 实例
scores = [] # 用于存储每轮交叉验证的准确率
for train_index, test_index in kfold.split(X):
X_train, X_test = X[train_index], X[test_index] # 划分训练集和测试集
y_train, y_test = y[train_index], y[test_index] # 划分对应的标签
y_pred = knn(X_train, y_train, X_test, k) # 进行 KNN 预测
accuracy = np.sum(y_pred == y_test) / len(y_test) # 计算准确率
scores.append(accuracy) # 添加到准确率列表中
return np.mean(scores) # 返回准确率的平均值
# 主函数
if __name__ == '__main__':
iris = load_iris() # 加载鸢尾花数据集
X = iris.data[:, :2] # 仅使用前两个特征
y = iris.target # 获取标签
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
k = 3 # 设定 KNN 中的 k 值
n_splits = 5 # 交叉验证的折数
mean_accuracy = cross_val_knn(X, y, k, n_splits) # 进行交叉验证
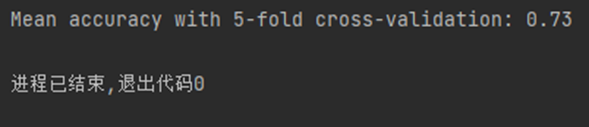
print(f"Mean accuracy with {n_splits}-fold cross-validation: {mean_accuracy:.2f}") # 输出交叉验证的平均准确率
# 可视化
plt.figure(figsize=(12, 6)) # 创建一个新的图像,设置大小为 12x6
# 绘制训练数据
for label, marker, color in zip(range(3), ('o', 's', '^'), ('blue', 'red', 'green')):
# 遍历三个类别,分别设置不同的标记和颜色
plt.scatter(X_train[y_train == label, 0], X_train[y_train == label, 1], marker=marker, color=color,
label=iris.target_names[label]) # 绘制每个类别的散点图
# 绘制测试数据
for label, marker, color in zip(range(3), ('D', 'P', 'X'), ('cyan', 'magenta', 'yellow')):
# 遍历三个类别,分别设置不同的标记和颜色
plt.scatter(X_test[y_test == label, 0], X_test[y_test == label, 1], marker=marker, color=color,
label=iris.target_names[label] + ' Test', edgecolors='black', linewidths=1, s=100)
# 绘制每个类别的测试数据散点图,使用黑色边缘突出显示,设置线宽为 1,点大小为 100
plt.xlabel('Sepal length') # 设置 x 轴标签为 Sepal length(萼片长度)
plt.ylabel('Sepal width') # 设置 y 轴标签为 Sepal width(萼片宽度)
plt.title('kNN Algorithm with k = 3') # 设置图像标题为 kNN Algorithm with k = 3
plt.legend() # 显示图例
plt.show() # 展示图像(2)运行结果
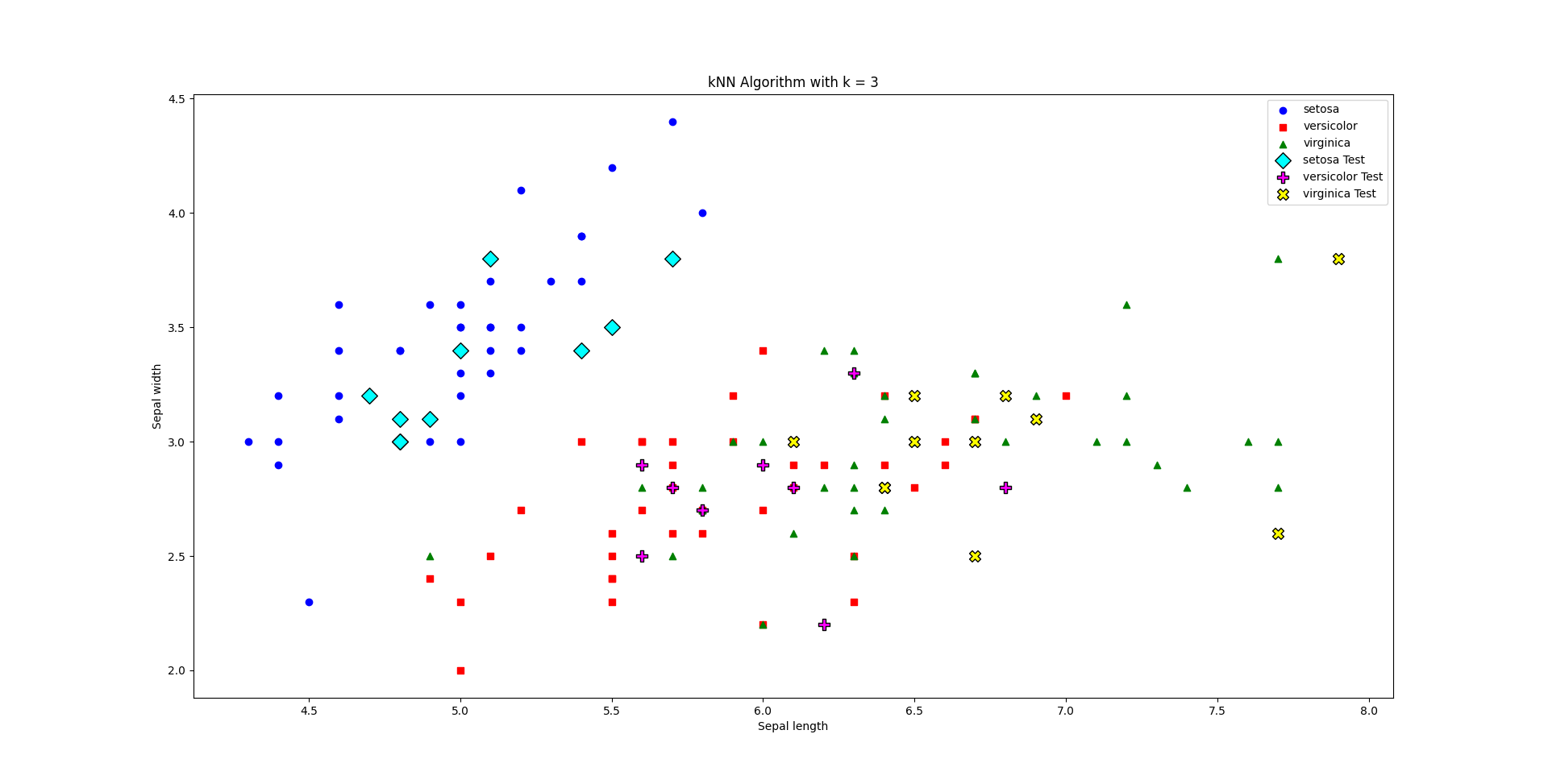
这个图像展示了预测数据与实际数据的对比。
三、分析实验结果
通过使用5折交叉验证(5-fold cross-validation)对 KNN 算法进行评估,得到的平均准确率(mean accuracy)为 0.73,即 73%。
交叉验证是一种评估模型泛化性能的方法,它将数据集分为多个子集,轮流将每个子集作为测试集,其余子集作为训练集。在实验中,我们使用了5折交叉验证,将数据集分为5个子集。对于每个子集,我们都训练并测试 KNN 模型,计算准确率,并将所有子集的准确率求平均得到最终的评估结果。
在实验中,KNN 模型在使用前两个特征(萼片长度和萼片宽度)对鸢尾花数据集进行分类时,平均准确率为 73%。这意味着 KNN 模型在这个特定任务中的性能表现较为一般,可能有很多原因导致准确率不高,例如:
- 特征选择:我们只使用了前两个特征(萼片长度和萼片宽度),而忽略了其他特征(花瓣长度和花瓣宽度)。这可能导致模型没有充分利用所有可用的信息进行预测。尝试使用更多或不同的特征组合可能会提高准确率。
- 参数选择:在实验中,我们设置了 KNN 算法的 k 值为 3。k 值的选择可能会影响模型的性能。为了找到最佳的 k 值,可以尝试对不同的 k 值进行交叉验证,选择具有最高准确率的 k 值。
- 数据预处理:在实验中,我们没有对数据进行预处理,例如归一化或标准化。预处理可以改善数据的分布,从而提高 KNN 算法的性能。
- 使用其他机器学习算法:KNN 算法可能不是解决这个问题的最佳算法。尝试其他的分类算法,如决策树、支持向量机或随机森林等,可能会得到更好的性能表现。
四、模型改进
为了尽可能提高 KNN 算法在 5 折交叉验证中的准确率,我们可以尝试以下改进方法:
- 使用全部特征:在原始代码中,我们只使用了前两个特征。为了提高准确率,我们可以使用全部四个特征。
- 数据预处理:对数据进行预处理,例如归一化或标准化,以便使得各个特征具有相同的量级。
- 调整 KNN 算法的参数:尝试使用不同的 k 值,并通过交叉验证选择最佳 k 值。
(1)改进后代码
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import pandas as pd
from tqdm import tqdm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split, KFold
from sklearn.preprocessing import StandardScaler
from collections import Counter
# 定义欧氏距离计算函数
def euclidean_distance(x1, x2):
return np.sqrt(np.sum((x1 - x2) ** 2))
# 定义 KNN 算法函数
def knn(X_train, y_train, X_test, k):
y_pred = [] # 初始化预测结果列表
for test_point in X_test:
distances = [] # 存储测试点到所有训练点的距离及其对应的标签
for train_point, label in zip(X_train, y_train):
dist = euclidean_distance(test_point, train_point) # 计算距离
distances.append((dist, label)) # 将距离和对应的标签添加到列表中
distances.sort(key=lambda x: x[0]) # 按距离升序排列
k_nearest_neighbors = [label for _, label in distances[:k]] # 获取前 k 个最近邻的标签
most_common = Counter(k_nearest_neighbors).most_common(1) # 找到出现次数最多的标签
y_pred.append(most_common[0][0]) # 添加到预测结果列表中
return y_pred
# 定义交叉验证函数
def cross_val_knn(X, y, k, n_splits):
kfold = KFold(n_splits=n_splits, shuffle=True, random_state=42) # 定义 KFold 实例
scores = [] # 用于存储每轮交叉验证的准确率
for train_index, test_index in kfold.split(X):
X_train, X_test = X[train_index], X[test_index] # 划分训练集和测试集
y_train, y_test = y[train_index], y[test_index] # 划分对应的标签
y_pred = knn(X_train, y_train, X_test, k) # 进行 KNN 预测
accuracy = np.sum(y_pred == y_test) / len(y_test) # 计算准确率
scores.append(accuracy) # 添加到准确率列表中
return np.mean(scores) # 返回准确率的平均值
# 主函数
if __name__ == '__main__':
iris = load_iris() # 加载鸢尾花数据集
X = iris.data # 使用全部四个特征
y = iris.target # 获取标签
# 数据预处理:标准化
scaler = StandardScaler()
X = scaler.fit_transform(X)
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 使用交叉验证选择最佳 k 值
best_k = 1
best_accuracy = 0
k_range = 21
n_splits = 5 # 交叉验证的折数
yellow_text = "\033[93m" # 使用 ANSI 转义码设置黄色文字
progress_bar = tqdm(range(1, k_range), desc=f"Finding best k", colour='green',
bar_format=f"{{l_bar}}{{bar}}{yellow_text}| {{n_fmt}}/{k_range - 1} {{postfix}}")
for k in progress_bar: # 尝试 k 值从 1 到 20
mean_accuracy = cross_val_knn(X, y, k, n_splits) # 进行交叉验证
if mean_accuracy > best_accuracy: # 寻找最佳 k 值
best_k = k
best_accuracy = mean_accuracy
progress_bar.set_postfix(
{f"k": k, f"Mean accuracy with {n_splits}-fold cross-validation": f"{mean_accuracy:.2f}"})
progress_bar.close()
# 重置终端颜色
print("\033[0m", end="")
print(f"Best k value: {best_k},with best mean accuracy: {best_accuracy:.2f}")
y_pred = knn(X_train, y_train, X_test, best_k) # 使用最佳 k 值进行预测
# 创建包含真实结果的 DataFrame
df_true = pd.DataFrame(X_test, columns=iris.feature_names)
df_true['label'] = y_test
# 创建包含预测结果的 DataFrame
df_pred = pd.DataFrame(X_test, columns=iris.feature_names)
df_pred['label'] = y_pred
# 绘制真实结果的分类散点图矩阵
g_true = sns.PairGrid(data=df_true, hue='label', vars=iris.feature_names)
g_true = g_true.map_diag(sns.kdeplot, lw=1, legend=False, fill=True)
g_true = g_true.map_offdiag(sns.scatterplot, edgecolor="w", s=40)
g_true.add_legend()
g_true.fig.subplots_adjust(top=0.9)
g_true.fig.suptitle('True Labels', fontsize=16)
plt.show(block=False)
# 绘制预测结果的分类散点图矩阵
g_pred = sns.PairGrid(data=df_pred, hue='label', vars=iris.feature_names)
g_pred = g_pred.map_diag(sns.kdeplot, lw=1, legend=False, fill=True)
g_pred = g_pred.map_offdiag(sns.scatterplot, edgecolor="w", s=40)
g_pred.add_legend()
g_pred.fig.subplots_adjust(top=0.9)
g_pred.fig.suptitle('Predicted Labels', fontsize=16)
plt.show()
(2)实验结果
通过二维分类散点图矩阵我们可以对测试数据的kNN算法预测结果与真实结果进行直观的比较:
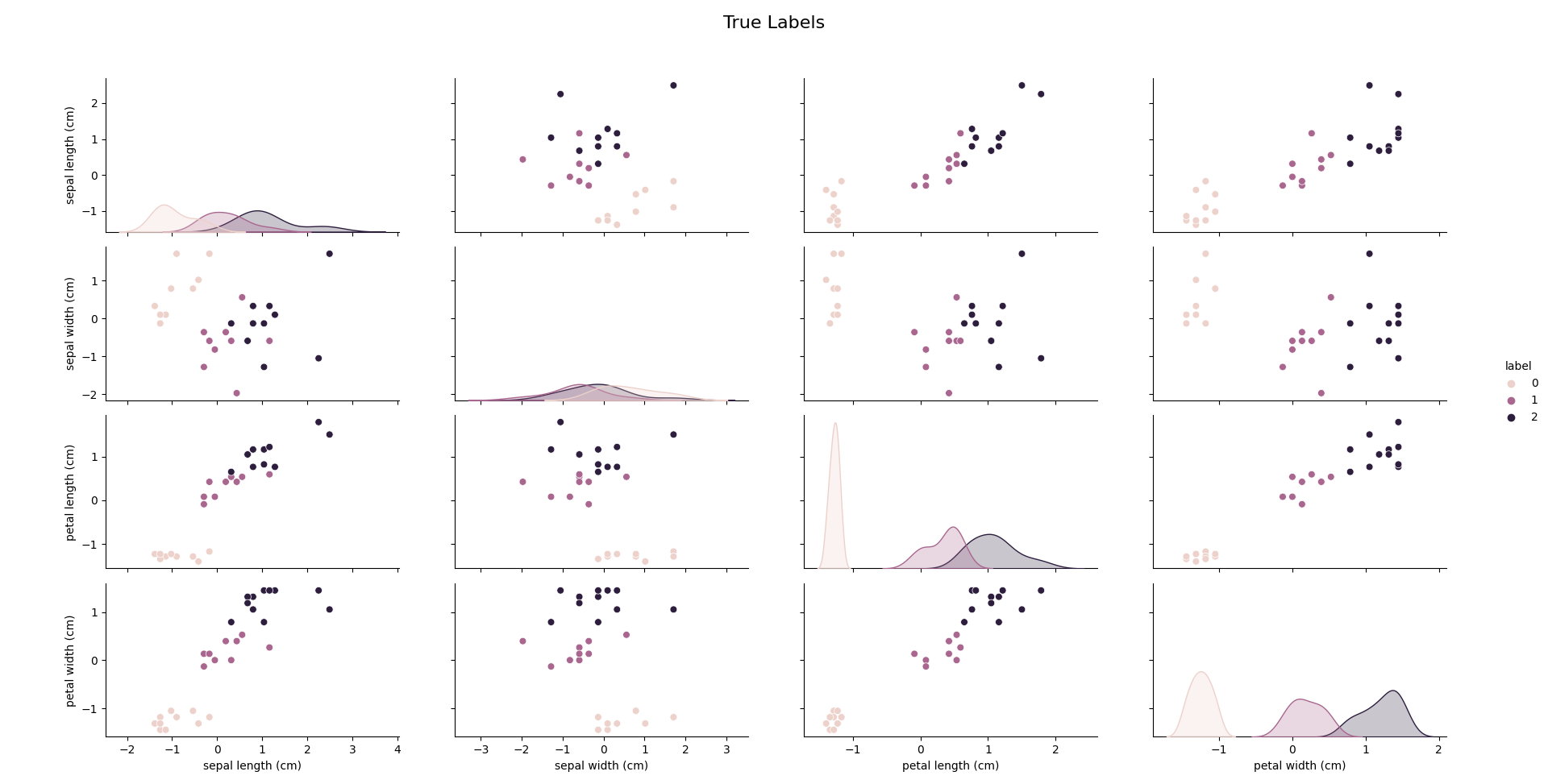
真实结果的分类散点图矩阵
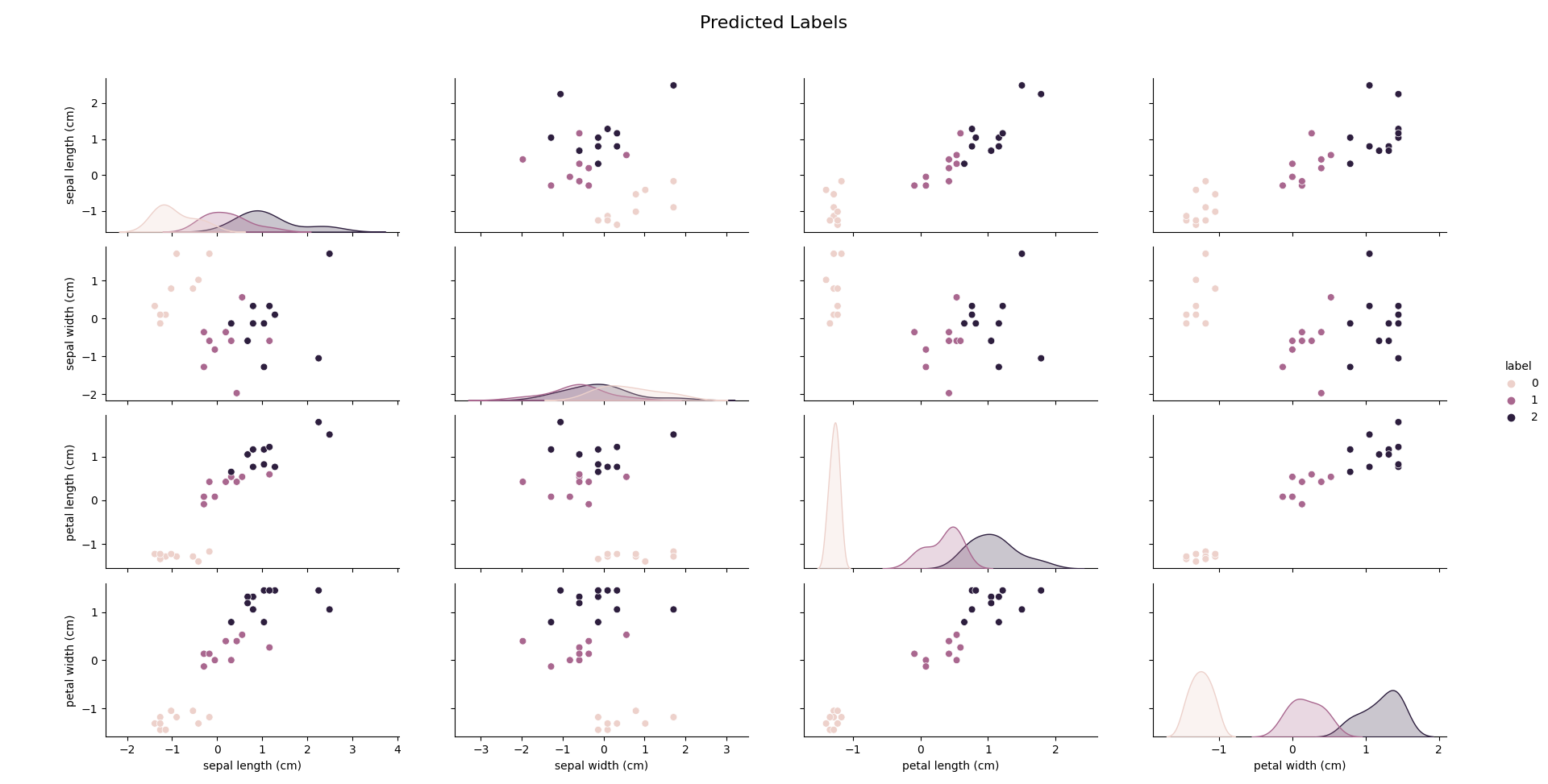
预测结果的分类散点图矩阵

控制台输出截图
(3)实验结果分析
改进后的模型使用5折交叉验证(5-fold cross-validation)对 KNN 算法进行评估,得到的平均准确率(mean accuracy)为 0.97,即 97%。使用鸢尾花全部四个特征,找到的最佳k值为11。通过数据可以看出,我们对模型的改进是非常成功的。
五、解决问题过程中对KNN的部分理解
KNN 算法是一种惰性学习方法,意味着在训练阶段并不会构建一个真正的模型。相反,它在预测阶段通过搜索训练数据集来找到距离新输入实例最近的 k 个训练样本。距离度量通常采用欧几里得距离、曼哈顿距离或其他相似性度量方法。确定 k 个最近邻居后,对于分类任务,算法会根据这些邻居的类别进行投票,选择投票结果中出现次数最多的类别作为预测结果;对于回归任务,算法会计算这些邻居的目标值的平均值或加权平均值(基于距离或其他权重)作为预测结果。
KNN 算法的性能在很大程度上取决于选择的邻居数量 k 和距离度量方法。一个合适的 k 值可以平衡过拟合(较小的 k 值)和欠拟合(较大的 k 值)的风险。通常,可以使用交叉验证来找到最佳的 k 值。KNN 算法对于特征缩放非常敏感。在应用 KNN 算法之前,建议对特征进行归一化或标准化处理,以确保每个特征在距离计算中具有相等的权重。
KNN 算法在处理大数据集时可能会面临计算效率和内存使用方面的挑战。为了提高性能,可以使用近似最近邻搜索技术,如 k-d 树、球树(ball tree)或局部敏感哈希(Locality-Sensitive Hashing, LSH)等。这些方法可以加快最近邻查找的速度,从而减少计算时间。
KNN 算法对噪声和不相关特征敏感。为了提高模型性能,可以考虑使用特征选择技术来减少不相关或冗余特征,从而减小模型的复杂度。
KNN 算法适用于较小的数据集和较少特征的情况。对于高维数据集,KNN 算法的性能可能会受到所谓的 "维数灾难" 的影响,即随着特征维数的增加,所有数据点之间的距离变得越来越相似,导致 KNN 算法的性能下降。在这种情况下,可以考虑使用降维技术,如主成分分析(PCA)或线性判别分析(LDA)等。

