线性回归实现 波士顿房价数据集

实验概述

本实验旨在评估和比较两种手动实现的回归方法（Normal Equation 和 SAG）在波士顿房价数据集上的性能。为了提供一个更全面的评估，我们将这两种方法与 sklearn 库中的线性回归模型和岭回归模型进行对比。通过对比不同回归方法在同一数据集上的表现，我们可以更好地了解各个方法的优劣以及适用场景。

实验流程

本实验流程如下：

• 数据准备：加载波士顿房价数据集，并将其划分为训练集和测试集。
• 特征缩放：使用 StandardScaler 对数据进行标准化。
• 实现Normal Equation：使用正规方程方法（Normal Equation）进行线性回归。
• 实现SAG：使用随机平均梯度下降（SAG）方法进行线性回归。

• 模型评估：

  • 绘制正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的 MSE 和 R² 比较图。
  • 绘制学习曲线对比正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的训练和交叉验证性能。
  • 绘制正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的残差图，以直观地展示四种方法在预测房价时产生的误差。
• 实验结果导出：将实验结果（包括均方误差、学习曲线数据和残差数据）导出到 JSON 文件。

实验涉及知识点

1. 数据获取与预处理：

   • 使用fetch_openml从OpenML加载波士顿房价数据集。
   • 使用Pandas创建特征DataFrame和目标Series。
   • 使用train_test_split将数据集分割为训练集和测试集。
   • 使用StandardScaler对数据进行标准化处理。

2. 模型选择与实现：

   • 使用正规方程方法求解线性回归模型。
   • 使用随机平均梯度下降（SAG）方法求解线性回归模型。
   • 使用Scikit-learn的线性回归（LinearRegression）模型。
   • 使用Scikit-learn的岭回归（Ridge）模型。

3. 模型训练：

   • 使用正规方程和SAG方法训练自定义线性回归模型。
   • 使用Scikit-learn训练线性回归和岭回归模型。

4. 模型评估：

   • 使用Mean Squared Error（MSE，均方误差）评估模型。
   • 使用R²（决定系数）评估模型。
   • 使用learning_curve函数进行交叉验证，评估模型在不同训练集大小下的性能。

5. 结果可视化：

   • 使用Matplotlib和Seaborn库进行可视化。
   • 绘制MSE和R²比较图。
   • 绘制学习曲线。
   • 绘制残差图。

实验环境

windows11、Python3.9、pycharm

实验代码实现

import numpy as np
import pandas as pd
from sklearn.datasets import fetch_openml
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error, r2_score
from sklearn.linear_model import LinearRegression, Ridge
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import learning_curve
import json


def load_boston_data():
    """
    加载波士顿房价数据集，并将其特征矩阵和目标向量返回。

    返回值：
        data (ndarray): 特征矩阵。
        target (ndarray): 目标向量。
    """
    # 加载波士顿房价数据集
    boston = fetch_openml(name='Boston', version=1, as_frame=True, parser='auto')
    # 创建特征 DataFrame
    data = pd.DataFrame(boston['data'], columns=boston['feature_names'])
    # 创建目标 Series
    target = pd.Series(boston['target'], name='MEDV')
    # 返回特征矩阵和目标向量
    return data.values, target.values


def normal_equation(X, y):
    """
    使用正规方程方法求解线性回归模型。

    参数：
        X (ndarray): 特征矩阵。
        y (ndarray): 目标向量。

    返回值：
        theta_best (ndarray): 最佳参数。
    """
    X_b = np.c_[np.ones((len(X), 1)), X]  # 添加偏置项
    theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y)  # 计算最佳参数
    return theta_best


def sag(X, y, alpha=0.001, n_epochs=1000):
    """
    使用SAG方法求解线性回归模型。

    参数：
        X (ndarray): 特征矩阵。
        y (ndarray): 目标向量。
        alpha (float): 学习率，默认为 0.001。
        n_epochs (int): 迭代次数，默认为 1000。

    返回值：
        theta (ndarray): 最佳参数。
    """
    m, n = X.shape
    X_b = np.c_[np.ones((m, 1)), X]  # 添加偏置项
    theta = np.random.randn(n + 1, 1)  # 初始化参数
    prev_gradients = np.zeros((n + 1, 1))  # 上一次迭代的梯度
    grad_hist = np.zeros((m, n + 1))  # 梯度历史记录
    for epoch in range(n_epochs):
        for i in range(m):
            random_index = np.random.randint(m)  # 随机选择一个样本
            xi = X_b[random_index:random_index + 1]
            yi = y[random_index:random_index + 1]
            gradients = 2 * xi.T.dot(xi.dot(theta) - yi)  # 计算梯度
            grad_hist[random_index] = gradients.flatten()  # 将梯度记录到梯度历史记录中
            avg_grad = np.mean(grad_hist, axis=0).reshape(-1, 1)  # 计算平均梯度
            if epoch == 0 and i == 0:
                prev_gradients = avg_grad  # 初始化上一次迭代的梯度
            delta_gradients = gradients - prev_gradients  # 计算梯度变化量
            theta = theta - alpha * avg_grad  # 更新参数
            prev_gradients = prev_gradients + delta_gradients / m  # 更新上一次迭代的梯度
    return theta


def plot_mse_r2_comparison(mse_normal, mse_sag, mse_sklearn_normal, mse_sklearn_sag, r2_normal, r2_sag,
                           r2_sklearn_normal, r2_sklearn_sag):
    """
    绘制正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的 MSE 和 R² 比较图。

    参数：
        mse_normal (float): 正规方程方法的 MSE。
        mse_sag (float): SAG 方法的 MSE。
        mse_sklearn_normal (float): sklearn 的线性回归模型的 MSE。
        mse_sklearn_sag (float): sklearn 的岭回归模型的 MSE。
        r2_normal (float): 正规方程方法的 R²。
        r2_sag (float): SAG 方法的 R²。
        r2_sklearn_normal (float): sklearn 的线性回归模型的 R²。
        r2_sklearn_sag (float): sklearn 的岭回归模型的 R²。
    """

    # 创建两个子图，一个用于绘制 MSE 比较图，另一个用于绘制 R² 比较图
    fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6), sharey=False)

    # 在 ax1 中绘制 MSE 比较图
    sns.barplot(x=["Custom Normal Equation", "Custom SAG", "Sklearn Normal Equation", "Sklearn SAG"],
                y=[mse_normal, mse_sag, mse_sklearn_normal, mse_sklearn_sag], ax=ax1)
    ax1.set_ylabel('Mean Squared Error')
    ax1.set_title('MSE Comparison')

    # 在 ax2 中绘制 R² 比较图
    sns.barplot(x=["Custom Normal Equation", "Custom SAG", "Sklearn Normal Equation", "Sklearn SAG"],
                y=[r2_normal, r2_sag, r2_sklearn_normal, r2_sklearn_sag], ax=ax2)
    ax2.set_ylabel('Coefficient of Determination (R²)')
    ax2.set_title('R² Comparison')

    plt.show(block=False)


def plot_learning_curves(models, model_names, X_train_scaled, y_train):
    """
    绘制学习曲线，用于比较不同模型的训练误差和验证误差。

    参数：
        models (list): 模型列表。
        model_names (list): 模型名称列表。
        X_train_scaled (ndarray): 标准化后的训练特征矩阵。
        y_train (ndarray): 训练目标向量。

    返回值：
        train_sizes (ndarray): 训练样本数量数组。
        train_scores_mean_all (ndarray): 平均训练分数数组。
        test_scores_mean_all (ndarray): 平均测试分数数组。
    """
    # 确保模型列表和模型名称列表的长度相等
    assert len(models) == len(model_names), "Number of models should be equal to number of model names"

    n = len(models)
    fig, axes = plt.subplots(1, n, figsize=(5 * n, 6), sharey=True)

    train_scores_mean_all = []
    test_scores_mean_all = []
    train_sizes = np.array([])

    for estimator, title, ax in zip(models, model_names, axes):
        # 使用 5 折交叉验证计算学习曲线
        train_sizes, train_scores, test_scores = learning_curve(
            estimator, X_train_scaled, y_train, train_sizes=np.linspace(0.1, 1.0, 10), cv=5,
            scoring="neg_mean_squared_error"
        )

        train_scores_mean = -np.mean(train_scores, axis=1)
        test_scores_mean = -np.mean(test_scores, axis=1)

        train_scores_mean_all.append(train_scores_mean)
        test_scores_mean_all.append(test_scores_mean)

        # 绘制训练误差和验证误差曲线
        ax.plot(train_sizes, train_scores_mean, 'o-', label="Training score")
        ax.plot(train_sizes, test_scores_mean, 'o-', label="Cross-validation score")
        ax.set_xlabel("Training examples")
        ax.set_ylabel("Mean Squared Error")
        ax.set_title(title)
        ax.legend(loc="best")
        ax.grid()

    plt.show(block=False)

    return train_sizes, np.array(train_scores_mean_all), np.array(test_scores_mean_all)


def plot_residuals_combined(y_test, y_preds, model_names):
    """
    绘制多个模型的真实值与残差的散点图。

    参数：
       y_test (ndarray): 测试目标向量。
       y_preds (list): 预测目标向量列表。
       model_names (list): 模型名称列表。
    """
    # 确保预测值列表的长度与模型名称列表的长度相等
    assert len(y_preds) == len(model_names), "Number of predictions should be equal to number of model names"

    n = len(y_preds)  # 获取预测值列表的长度（模型数量）

    # 创建 1 x n 的子图，宽高比为 5 * n 和 6，共享 y 轴
    fig, axes = plt.subplots(1, n, figsize=(5 * n, 6), sharey=True)

    # 遍历预测值、模型名称和子图的轴
    for y_pred, title, ax in zip(y_preds, model_names, axes):
        residuals = y_test - y_pred.reshape(-1)  # 计算残差
        ax.scatter(y_test, residuals)  # 绘制真实值与残差的散点图
        ax.axhline(y=0, color='r', linestyle='--')  # 绘制 y=0 的水平虚线
        ax.set_xlabel("True Values")  # 设置 x 轴标签
        ax.set_ylabel("Residuals")  # 设置 y 轴标签
        ax.set_title(title)  # 设置子图标题
        ax.grid()  # 显示网格线

    plt.show()  # 展示图像


def export_data(mse_normal, mse_sag, mse_sklearn_normal, mse_sklearn_sag,
                r2_normal, r2_sag, r2_sklearn_normal, r2_sklearn_sag,
                learning_curve_data, residuals_data, file_name):
    """
    导出模型评估指标和图形数据到 JSON 文件。

    参数：
        mse_normal (float): 正规方程方法的 MSE。
        mse_sag (float): SAG 方法的 MSE。
        mse_sklearn_normal (float): sklearn 的线性回归模型的 MSE。
        mse_sklearn_sag (float): sklearn 的岭回归模型的 MSE。
        r2_normal (float): 正规方程方法的 R²。
        r2_sag (float): SAG 方法的 R²。
        r2_sklearn_normal (float): sklearn 的线性回归模型的 R²。
        r2_sklearn_sag (float): sklearn 的岭回归模型的 R²。
        learning_curve_data (dict): 学习曲线数据。
        residuals_data (dict): 残差数据。
        file_name (str): JSON 文件名。
    """
    data = {
        "mse": {
            "normal_equation": mse_normal,
            "sag": mse_sag,
            "sklearn_linear_regression": mse_sklearn_normal,
            "sklearn_ridge_regression_sag": mse_sklearn_sag
        },
        "r2": {
            "normal_equation": r2_normal,
            "sag": r2_sag,
            "sklearn_linear_regression": r2_sklearn_normal,
            "sklearn_ridge_regression_sag": r2_sklearn_sag
        },
        "learning_curve": learning_curve_data,
        "residuals": residuals_data
    }

    with open(file_name, 'w') as outfile:
        json.dump(data, outfile)


def main():
    """
    执行主要操作的 Python 脚本的主函数。

    参数：
       无

    返回值：
       无

    说明：
       本函数主要实现波士顿房价数据集的预处理、模型训练和评估，并将结果导出到 JSON 文件中。
       具体步骤包括：
       1. 载入并预处理数据集。
       2. 利用正规方程、SAG 方法和 sklearn 的线性回归模型和岭回归模型进行模型训练和评估，计算 MSE 和 R²。
       3. 绘制正规方程、SAG 方法和 sklearn 的线性回归模型和岭回归模型的学习曲线和真实值与残差的散点图。
       4. 导出模型评估指标和图形数据到 JSON 文件。

    示例：
       main()
    """
    # 加载波士顿房价数据
    X, y = load_boston_data()
    # 将数据集分割为训练集和测试集
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=20)

    # 使用 StandardScaler 对数据进行标准化
    scaler = StandardScaler()
    X_train_scaled = scaler.fit_transform(X_train)
    X_test_scaled = scaler.transform(X_test)

    # 使用正规方程方法进行线性回归
    theta_normal = normal_equation(X_train_scaled, y_train)
    X_test_normal = np.c_[np.ones((len(X_test_scaled), 1)), X_test_scaled]
    y_pred_normal = X_test_normal.dot(theta_normal)

    # 使用 sklearn 的线性回归模型（正规方程）
    sklearn_normal_estimator = LinearRegression()
    sklearn_normal_estimator.fit(X_train_scaled, y_train)
    y_pred_sklearn_normal = sklearn_normal_estimator.predict(X_test_scaled)

    # 使用 SAG 方法进行线性回归
    theta_sag = sag(X_train_scaled, y_train)
    X_test_sag = np.c_[np.ones((len(X_test_scaled), 1)), X_test_scaled]
    y_pred_sag = X_test_sag.dot(theta_sag)

    # 使用 sklearn 的岭回归模型（SAG）
    sklearn_sag_estimator = Ridge(solver="sag", random_state=42)
    sklearn_sag_estimator.fit(X_train_scaled, y_train)
    y_pred_sklearn_sag = sklearn_sag_estimator.predict(X_test_scaled)

    # 计算正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的均方误差
    mse_normal = mean_squared_error(y_test, y_pred_normal)
    mse_sag = mean_squared_error(y_test, y_pred_sag)
    mse_sklearn_normal = mean_squared_error(y_test, y_pred_sklearn_normal)
    mse_sklearn_sag = mean_squared_error(y_test, y_pred_sklearn_sag)

    # 计算正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的决定系数
    r2_normal = r2_score(y_test, y_pred_normal)
    r2_sag = r2_score(y_test, y_pred_sag)
    r2_sklearn_normal = sklearn_normal_estimator.score(X_test_scaled, y_test)
    r2_sklearn_sag = sklearn_sag_estimator.score(X_test_scaled, y_test)

    # 打印正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的均方误差
    print("Normal Equation MSE:", mse_normal)
    print("Sklearn Linear Regression MSE:", mse_sklearn_normal)
    print("SAG MSE:", mse_sag)
    print("Sklearn Ridge Regression (SAG) MSE:", mse_sklearn_sag)

    # 打印正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的决定系数
    print("Normal Equation R²:", r2_normal)
    print("Sklearn Linear Regression R²:", r2_sklearn_normal)
    print("SAG R²:", r2_sag)
    print("Sklearn Ridge Regression (SAG) R²:", r2_sklearn_sag)

    # 绘制正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的 MSE 和 R² 比较图
    plot_mse_r2_comparison(mse_normal, mse_sag, mse_sklearn_normal, mse_sklearn_sag, r2_normal, r2_sag,
                           r2_sklearn_normal, r2_sklearn_sag)

    # 创建模型实例
    normal_estimator = LinearRegression()
    sag_estimator = Ridge(solver="sag", random_state=42)
    sklearn_normal_estimator = LinearRegression()
    sklearn_sag_estimator = Ridge(solver="sag", random_state=42)

    # 拟合模型
    normal_estimator.fit(X_train_scaled, y_train)
    sag_estimator.fit(X_train_scaled, y_train)
    sklearn_normal_estimator.fit(X_train_scaled, y_train)
    sklearn_sag_estimator.fit(X_train_scaled, y_train)

    # 绘制学习曲线
    train_sizes, train_scores_mean_all, test_scores_mean_all = plot_learning_curves(
        [normal_estimator, sag_estimator, sklearn_normal_estimator, sklearn_sag_estimator],
        ["Normal Equation", "SAG", "Sklearn Linear Regression", "Sklearn Ridge Regression (SAG)"],
        X_train_scaled, y_train
    )

    train_scores_normal, train_scores_sag, train_scores_sklearn_normal, train_scores_sklearn_sag = train_scores_mean_all
    test_scores_normal, test_scores_sag, test_scores_sklearn_normal, test_scores_sklearn_sag = test_scores_mean_all

    # 绘制残差图
    plot_residuals_combined(
        y_test,
        [y_pred_normal, y_pred_sag, y_pred_sklearn_normal, y_pred_sklearn_sag],
        ["Normal Equation", "SAG", "Sklearn Linear Regression", "SklearnRidge Regression (SAG)"]
    )

    # 收集学习曲线数据
    learning_curve_data = {
        "normal_equation": {
            "train_sizes": train_sizes.tolist(),
            "train_scores": (-train_scores_normal).tolist(),
            "test_scores": (-test_scores_normal).tolist()
        },
        "sag": {
            "train_sizes": train_sizes.tolist(),
            "train_scores": (-train_scores_sag).tolist(),
            "test_scores": (-test_scores_sag).tolist()
        },
        "sklearn_linear_regression": {
            "train_sizes": train_sizes.tolist(),
            "train_scores": (-train_scores_sklearn_normal).tolist(),
            "test_scores": (-test_scores_sklearn_normal).tolist()
        },
        "sklearn_ridge_regression_sag": {
            "train_sizes": train_sizes.tolist(),
            "train_scores": (-train_scores_sklearn_sag).tolist(),
            "test_scores": (-test_scores_sklearn_sag).tolist()
        }
    }

    # 收集残差数据
    residuals_data = {
        "normal_equation": {
            "y_test": y_test.tolist(),
            "residuals": (y_test - y_pred_normal.reshape(-1)).tolist()
        },
        "sag": {
            "y_test": y_test.tolist(),
            "residuals": (y_test - y_pred_sag.reshape(-1)).tolist()
        },
        "sklearn_linear_regression": {
            "y_test": y_test.tolist(),
            "residuals": (y_test - y_pred_sklearn_normal.reshape(-1)).tolist()
        },
        "sklearn_ridge_regression_sag": {
            "y_test": y_test.tolist(),
            "residuals": (y_test - y_pred_sklearn_sag.reshape(-1)).tolist()
        }
    }

    # 导出数据到 JSON 文件
    export_data(
        mse_normal, mse_sag, mse_sklearn_normal, mse_sklearn_sag,
        r2_normal, r2_sag, r2_sklearn_normal, r2_sklearn_sag,
        learning_curve_data, residuals_data, "experiment_data.json"
    )


if __name__ == '__main__':
    main()

实验结果

控制台输出如下：

Normal Equation MSE: 16.495351975931648
Sklearn Linear Regression MSE: 16.49535197593168
SAG MSE: 16.495351975930593
Sklearn Ridge Regression (SAG) MSE: 16.49403693758767
Normal Equation R²: 0.7438826183113537
Sklearn Linear Regression R²: 0.7438826183113533
SAG R²: 0.74388261831137
Sklearn Ridge Regression (SAG) R²: 0.7439030364375006

绘制图像：

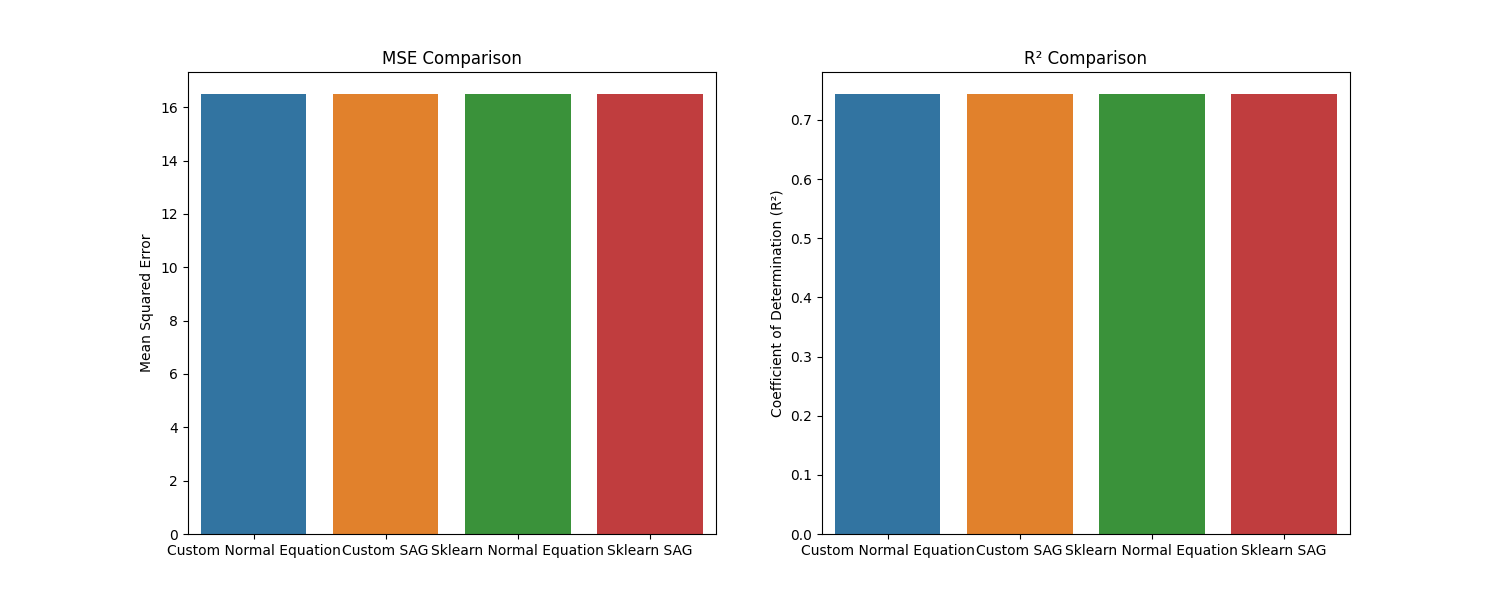
1. 正规方程、SAG 方法与 sklearn 的线性回归模型和岭回归模型的 MSE 和 R² 比较图：

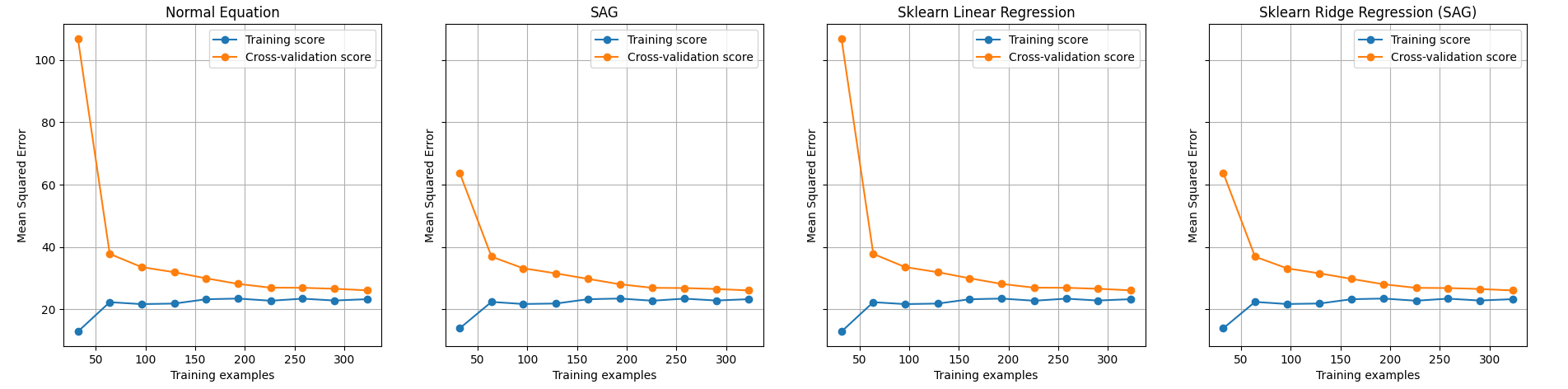
2. 绘制学习曲线：

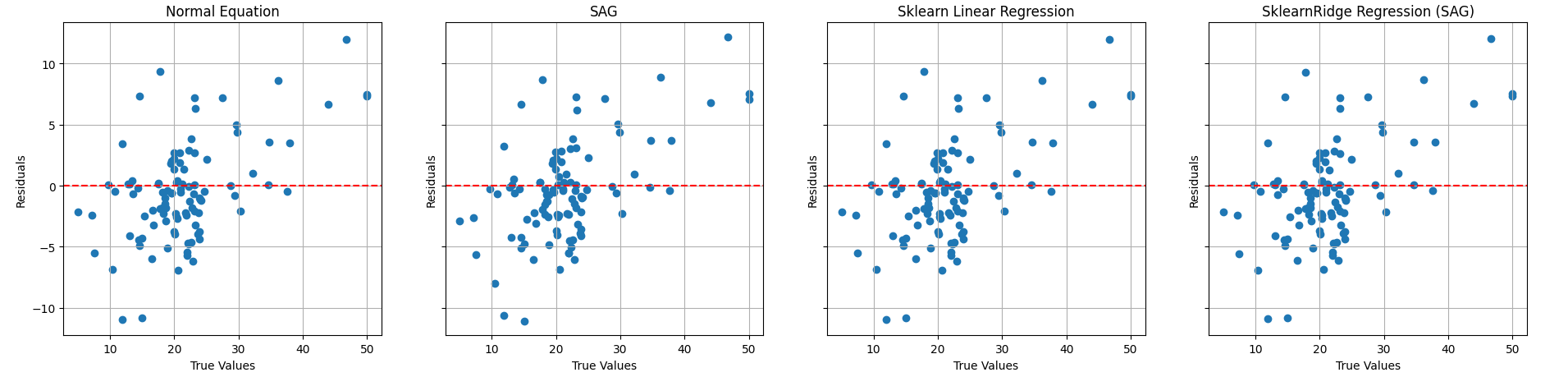
3. 绘制残差图：

导出JSON数据：

{"mse": {"normal_equation": 16.495351975931648, "sag": 16.495351975930593, "sklearn_linear_regression": 16.49535197593168, "sklearn_ridge_regression_sag": 16.49403693758767}, "r2": {"normal_equation": 0.7438826183113537, "sag": 0.74388261831137, "sklearn_linear_regression": 0.7438826183113533, "sklearn_ridge_regression_sag": 0.7439030364375006}, "learning_curve": {"normal_equation": {"train_sizes": [32, 64, 96, 129, 161, 193, 226, 258, 290, 323], "train_scores": [-12.910351098705954, -22.33333894680602, -21.71070548951119, -21.888101644813634, -23.269112479957673, -23.488177910312064, -22.79738397077156, -23.45699206861381, -22.864260231877733, -23.291469940532856], "test_scores": [-106.77489800166657, -37.809887012203106, -33.587412004823804, -31.933447197952233, -29.983361730560592, -28.188695913932055, -26.97815017884845, -26.94709218691517, -26.6289832419603, -26.13304648546775]}, "sag": {"train_sizes": [32, 64, 96, 129, 161, 193, 226, 258, 290, 323], "train_scores": [-13.94888357186779, -22.420926806046673, -21.744138802267518, -21.905593307444597, -23.280191466054806, -23.496238519829507, -22.802380013002427, -23.461549567875316, -22.867730560163334, -23.29388283950023], "test_scores": [-63.77411302266902, -36.91505940731197, -33.194861026354715, -31.550448648497866, -29.802517337663925, -28.08224500731423, -26.92384264091774, -26.860106325885262, -26.558238536260536, -26.09461385756405]}, "sklearn_linear_regression": {"train_sizes": [32, 64, 96, 129, 161, 193, 226, 258, 290, 323], "train_scores": [-12.910351098705954, -22.33333894680602, -21.71070548951119, -21.888101644813634, -23.269112479957673, -23.488177910312064, -22.79738397077156, -23.45699206861381, -22.864260231877733, -23.291469940532856], "test_scores": [-106.77489800166657, -37.809887012203106, -33.587412004823804, -31.933447197952233, -29.983361730560592, -28.188695913932055, -26.97815017884845, -26.94709218691517, -26.6289832419603, -26.13304648546775]}, "sklearn_ridge_regression_sag": {"train_sizes": [32, 64, 96, 129, 161, 193, 226, 258, 290, 323], "train_scores": [-13.94888357186779, -22.420926806046673, -21.744138802267518, -21.905593307444597, -23.280191466054806, -23.496238519829507, -22.802380013002427, -23.461549567875316, -22.867730560163334, -23.29388283950023], "test_scores": [-63.77411302266902, -36.91505940731197, -33.194861026354715, -31.550448648497866, -29.802517337663925, -28.08224500731423, -26.92384264091774, -26.860106325885262, -26.558238536260536, -26.09461385756405]}}, "residuals": {"normal_equation": {"y_test": [21.2, 20.6, 21.5, 21.7, 13.4, 20.4, 20.0, 5.0, 14.5, 24.0, 36.2, 23.1, 23.0, 21.0, 19.5, 24.7, 32.2, 14.6, 14.3, 17.5, 37.6, 50.0, 22.6, 30.3, 23.3, 22.1, 18.2, 23.1, 21.0, 21.9, 27.5, 19.9, 20.3, 7.2, 29.4, 18.6, 50.0, 22.2, 18.5, 34.7, 11.9, 23.2, 10.4, 13.1, 25.0, 28.7, 18.7, 23.1, 9.7, 7.5, 46.7, 34.6, 10.8, 44.0, 15.0, 20.2, 20.3, 16.8, 17.8, 23.1, 23.7, 19.6, 22.2, 18.9, 19.4, 16.6, 22.0, 15.0, 19.9, 15.4, 37.9, 17.5, 24.1, 20.4, 18.3, 23.9, 22.4, 22.0, 22.9, 20.8, 17.8, 13.5, 16.5, 14.6, 23.9, 29.6, 20.1, 20.8, 22.8, 22.3, 20.0, 29.8, 18.2, 12.8, 11.9, 23.9, 18.5, 18.9, 13.0, 22.6, 19.5, 23.8], "residuals": [0.1430923802065216, -6.944101920840463, 1.3376775158807988, -2.2188546488518526, 0.3958321755484615, 0.4283504207634259, 2.2541447511633486, -2.143935957153385, -4.415500720360992, -1.1438800868384966, 8.619003489658702, 7.232004321356019, -0.6692487337568203, -0.5083244475150366, -0.6274589595095925, -0.44885920857394623, 1.0029729125878184, -4.9166423444941625, -0.21270677707484253, 0.1361119458620017, -0.4683729401985701, 7.457367805346898, -4.625763941556304, -2.1117963239347866, -3.228570191307316, -4.727098837080931, -1.787709455662558, -2.0528370646136267, -0.28068136333954286, -2.444167255635328, 7.225181543199735, 2.660921751317659, -2.5226945132855825, -2.3870056152544388, -0.7895549688850245, -1.8016581778755487, 7.34960463865599, -0.0792612435666733, -1.0113265603931865, 3.565245583875445, 3.4564118065272975, 6.350717090546716, -6.87751358025873, 0.1414403557688093, 2.1711907284234293, 0.00013801165530580306, -2.8726123607729903, 2.67777583220893, 0.046604703818054816, -5.542644694813806, 11.999926086730234, 0.05780412244848776, -0.4610188661893311, 6.649143714885639, -4.333209642750674, -2.2985381623214955, 0.28225982137595196, -3.2334588670544804, -1.8495669882954218, 0.0667287209992331, -3.982949315204099, -0.5859752328219301, 2.8696015685118432, -5.0995630602617865, 1.8310812434225205, -2.033798915828225, -5.6849037312111435, -10.802780392812746, 1.3572401369693097, -2.5067714077725416, 3.508811007505024, 0.22622393119395667, -1.2000541232668134, -2.690879372956438, -2.3171809498852447, -1.011944956858457, -1.298617083283606, -5.429485668610827, -6.217124545905548, 2.6905731974967644, 9.339873744943759, -0.682026878065777, -5.949911652309037, 7.359978095162516, -4.386185447977425, 4.956234390182541, -3.975750789012512, 1.8780634423053932, -1.7820415068864648, -4.782905815128025, -3.7321922159998238, 4.375334053622499, -0.5277916714195854, 0.15988808153094247, -10.928859265029415, -3.776150175291729, -1.4611050117412105, -0.39762541067528545, -4.07612384974761, 3.8509254196426426, 2.027308218270548, -2.2051410693274]}, "sag": {"y_test": [21.2, 20.6, 21.5, 21.7, 13.4, 20.4, 20.0, 5.0, 14.5, 24.0, 36.2, 23.1, 23.0, 21.0, 19.5, 24.7, 32.2, 14.6, 14.3, 17.5, 37.6, 50.0, 22.6, 30.3, 23.3, 22.1, 18.2, 23.1, 21.0, 21.9, 27.5, 19.9, 20.3, 7.2, 29.4, 18.6, 50.0, 22.2, 18.5, 34.7, 11.9, 23.2, 10.4, 13.1, 25.0, 28.7, 18.7, 23.1, 9.7, 7.5, 46.7, 34.6, 10.8, 44.0, 15.0, 20.2, 20.3, 16.8, 17.8, 23.1, 23.7, 19.6, 22.2, 18.9, 19.4, 16.6, 22.0, 15.0, 19.9, 15.4, 37.9, 17.5, 24.1, 20.4, 18.3, 23.9, 22.4, 22.0, 22.9, 20.8, 17.8, 13.5, 16.5, 14.6, 23.9, 29.6, 20.1, 20.8, 22.8, 22.3, 20.0, 29.8, 18.2, 12.8, 11.9, 23.9, 18.5, 18.9, 13.0, 22.6, 19.5, 23.8], "residuals": [0.14309238020590698, -6.944101920838907, 1.3376775158804861, -2.2188546488521474, 0.39583217554860717, 0.42835042076369945, 2.2541447511637074, -2.143935957154145, -4.4155007203605905, -1.1438800868377825, 8.619003489659125, 7.232004321354502, -0.6692487337566391, -0.5083244475152284, -0.6274589595089992, -0.44885920857355543, 1.0029729125874418, -4.916642344493502, -0.21270677707509122, 0.13611194586193776, -0.46837294019807274, 7.4573678053471895, -4.625763941556521, -2.1117963239349926, -3.228570191306936, -4.727098837080586, -1.7877094556621707, -2.0528370646131577, -0.2806813633395855, -2.444167255634653, 7.225181543199799, 2.66092175131811, -2.522694513283678, -2.387005615255265, -0.789554968885259, -1.8016581778757512, 7.349604638655187, -0.0792612435660125, -1.0113265603923765, 3.5652455838758677, 3.4564118065286014, 6.350717090546841, -6.877513580260013, 0.1414403557689763, 2.1711907284240795, 0.00013801165652793657, -2.872612360772223, 2.6777758322086953, 0.04660470381839943, -5.542644694814655, 11.999926086729523, 0.05780412244837407, -0.46101886618950694, 6.649143714886279, -4.333209642750333, -2.2985381623206997, 0.28225982137721317, -3.2334588670542885, -1.849566988295713, 0.06672872099983707, -3.982949315202749, -0.5859752328219905, 2.869601568511822, -5.0995630602611755, 1.8310812434233377, -2.0337989158275676, -5.684903731211126, -10.802780392812899, 1.357240136969697, -2.5067714077726375, 3.50881100750577, 0.2262239311938572, -1.2000541232672717, -2.6908793729558695, -2.317180949885568, -1.0119449568583896, -1.2986170832841069, -5.4294856686104715, -6.217124545904365, 2.6905731974982885, 9.339873744942617, -0.6820268780661998, -5.949911652310398, 7.359978095161464, -4.3861854479774, 4.956234390182804, -3.9757507890114425, 1.8780634423066687, -1.7820415068860989, -4.78290581512719, -3.73219221599944, 4.375334053622737, -0.5277916714194077, 0.15988808153094425, -10.928859265029073, -3.7761501752909616, -1.461105011740301, -0.3976254106744648, -4.0761238497475425, 3.8509254196430938, 2.027308218269887, -2.2051410693269027]}, "sklearn_linear_regression": {"y_test": [21.2, 20.6, 21.5, 21.7, 13.4, 20.4, 20.0, 5.0, 14.5, 24.0, 36.2, 23.1, 23.0, 21.0, 19.5, 24.7, 32.2, 14.6, 14.3, 17.5, 37.6, 50.0, 22.6, 30.3, 23.3, 22.1, 18.2, 23.1, 21.0, 21.9, 27.5, 19.9, 20.3, 7.2, 29.4, 18.6, 50.0, 22.2, 18.5, 34.7, 11.9, 23.2, 10.4, 13.1, 25.0, 28.7, 18.7, 23.1, 9.7, 7.5, 46.7, 34.6, 10.8, 44.0, 15.0, 20.2, 20.3, 16.8, 17.8, 23.1, 23.7, 19.6, 22.2, 18.9, 19.4, 16.6, 22.0, 15.0, 19.9, 15.4, 37.9, 17.5, 24.1, 20.4, 18.3, 23.9, 22.4, 22.0, 22.9, 20.8, 17.8, 13.5, 16.5, 14.6, 23.9, 29.6, 20.1, 20.8, 22.8, 22.3, 20.0, 29.8, 18.2, 12.8, 11.9, 23.9, 18.5, 18.9, 13.0, 22.6, 19.5, 23.8], "residuals": [0.1430923802065145, -6.944101920840431, 1.337677515880788, -2.218854648851835, 0.3958321755484544, 0.428350420763433, 2.2541447511633557, -2.143935957153433, -4.415500720360988, -1.1438800868384718, 8.61900348965873, 7.232004321356008, -0.6692487337568025, -0.5083244475150295, -0.6274589595095605, -0.4488592085739356, 1.0029729125878433, -4.9166423444941625, -0.2127067770748674, 0.13611194586200526, -0.4683729401985346, 7.457367805346962, -4.6257639415563006, -2.1117963239347723, -3.2285701913072984, -4.7270988370809235, -1.7877094556625543, -2.0528370646136125, -0.28068136333953575, -2.444167255635321, 7.225181543199721, 2.660921751317666, -2.52269451328554, -2.3870056152544654, -0.7895549688850139, -1.8016581778755665, 7.349604638656018, -0.07926124356663777, -1.0113265603931545, 3.565245583875459, 3.4564118065272726, 6.35071709054672, -6.877513580258848, 0.1414403557687791, 2.171190728423465, 0.00013801165533067206, -2.8726123607729583, 2.6777758322089333, 0.04660470381804949, -5.542644694813818, 11.999926086730255, 0.05780412244850197, -0.4610188661893382, 6.649143714885689, -4.33320964275066, -2.298538162321492, 0.28225982137596617, -3.233458867054477, -1.8495669882954253, 0.06672872099924732, -3.982949315204092, -0.5859752328219514, 2.869601568511861, -5.099563060261765, 1.8310812434225419, -2.0337989158282, -5.684903731211136, -10.802780392812757, 1.3572401369693168, -2.5067714077725416, 3.5088110075050523, 0.22622393119394246, -1.200054123266824, -2.69087937295642, -2.317180949885266, -1.0119449568584429, -1.2986170832835988, -5.429485668610798, -6.21712454590552, 2.6905731974967644, 9.339873744943745, -0.682026878065777, -5.949911652309087, 7.359978095162502, -4.386185447977418, 4.956234390182573, -3.975750789012487, 1.8780634423053897, -1.7820415068864577, -4.782905815128039, -3.7321922159998344, 4.375334053622506, -0.5277916714195818, 0.15988808153094425, -10.928859265029411, -3.7761501752917077, -1.4611050117411928, -0.39762541067527124, -4.07612384974761, 3.8509254196426497, 2.0273082182705373, -2.205141069327386]}, "sklearn_ridge_regression_sag": {"y_test": [21.2, 20.6, 21.5, 21.7, 13.4, 20.4, 20.0, 5.0, 14.5, 24.0, 36.2, 23.1, 23.0, 21.0, 19.5, 24.7, 32.2, 14.6, 14.3, 17.5, 37.6, 50.0, 22.6, 30.3, 23.3, 22.1, 18.2, 23.1, 21.0, 21.9, 27.5, 19.9, 20.3, 7.2, 29.4, 18.6, 50.0, 22.2, 18.5, 34.7, 11.9, 23.2, 10.4, 13.1, 25.0, 28.7, 18.7, 23.1, 9.7, 7.5, 46.7, 34.6, 10.8, 44.0, 15.0, 20.2, 20.3, 16.8, 17.8, 23.1, 23.7, 19.6, 22.2, 18.9, 19.4, 16.6, 22.0, 15.0, 19.9, 15.4, 37.9, 17.5, 24.1, 20.4, 18.3, 23.9, 22.4, 22.0, 22.9, 20.8, 17.8, 13.5, 16.5, 14.6, 23.9, 29.6, 20.1, 20.8, 22.8, 22.3, 20.0, 29.8, 18.2, 12.8, 11.9, 23.9, 18.5, 18.9, 13.0, 22.6, 19.5, 23.8], "residuals": [0.1144086587948685, -6.852849721175492, 1.2802094304648222, -2.2110376764464945, 0.4168178246967216, 0.39650135758257576, 2.260427976818452, -2.180216539442341, -4.435952987902244, -1.1154445102518231, 8.65764990027159, 7.172219626938187, -0.690886986970142, -0.5415093323491114, -0.6351419665400435, -0.4831047702154656, 1.0031543484735295, -4.8841962696052565, -0.233021619531117, 0.10279479735874375, -0.4277950563503268, 7.546753082329509, -4.63194260050355, -2.1199913075242556, -3.201855745482547, -4.710617669986437, -1.8121915443624381, -2.0518188350569417, -0.2989117287084184, -2.4685545412095067, 7.257944325355499, 2.665694909405204, -2.415241737320617, -2.4109365226459056, -0.7886639309403378, -1.8183820753879658, 7.361260703869732, -0.10446850126502838, -1.0205120544848043, 3.5668716185751776, 3.4936504556699752, 6.350433657378172, -6.946983086591283, 0.08792256743413596, 2.154909436417647, 0.050447124932347265, -2.868221641416845, 2.63731570685475, 0.048939764306503264, -5.559709663296715, 12.007091828089429, 0.053196071773136566, -0.4824289671014981, 6.715853230406964, -4.364931969994188, -2.2937867904694684, 0.30043332125793043, -3.2504726014295997, -1.884511089463551, 0.09172144120868353, -3.924935406386826, -0.6031155502304344, 2.840842808659648, -5.078989115553739, 1.8257998968650284, -2.034810975626602, -5.685430131091444, -10.791391685233666, 1.3451654952182963, -2.521377476997925, 3.558453706493431, 0.13154235762399225, -1.2138889996555662, -2.6922287952326904, -2.337331088361932, -1.01875183243461, -1.3136436407949859, -5.42188820373071, -6.134565529969265, 2.7074628681915733, 9.256831086323382, -0.7174892312621086, -6.089409237491374, 7.279215572526859, -4.380627975660246, 4.978105177546521, -3.953953049968039, 1.9260986025418099, -1.776567080768821, -4.752702341138026, -3.7232942142902274, 4.399431915672544, -0.5473885838657253, 0.14683754631437473, -10.925565547540701, -3.755638936902699, -1.456345486909111, -0.42263034777570496, -4.082288274225512, 3.8363538027660056, 2.006532635585554, -2.200687279094076]}}}

结果分析

均方误差（MSE）和决定系数（R2）

从结果中，我们可以看出各个模型的表现如下：

1. 正规方程（Normal Equation）：MSE = 16.495，R2 = 0.7439
2. SAG（随机平均梯度下降）：MSE = 16.495，R2 = 0.7439
3. sklearn线性回归（Sklearn Linear Regression）：MSE = 16.495，R2 = 0.7439
4. sklearn岭回归SAG（Sklearn Ridge Regression SAG）：MSE = 16.494，R2 = 0.7439

从这些指标来看，四个模型的表现非常接近。其中，Sklearn岭回归SAG的MSE略低于其他模型，而R²得分与其他模型相近。这表明所有模型在预测上的性能相差不大，均具有较好的预测效果。

学习曲线

根据训练集和测试集的得分，我们发现，随着训练样本数量的增加，训练集和测试集的得分逐渐接近。这说明所有模型在面对更多的训练数据时，泛化能力得到了提高。此外，四个模型在不同训练集大小下的表现也相当接近，表明各模型在学习过程中的稳定性和性能相差无几。

残差

从残差分布来看，大部分模型的残差都集中在0附近，说明模型的预测与实际值相差不大。这进一步证实了所有模型在预测性能上的优势。

总结

综上所述，在本次实验中，四个模型的表现非常接近，均具有较好的预测效果。根据MSE和R²的指标，Sklearn岭回归SAG的表现略优于其他模型。从学习曲线来看，所有模型在面对更多的训练数据时，泛化能力得到了提高。在残差分析中，各模型的预测与实际值相差不大，进一步证实了模型的预测性能。

拓展延伸

学习曲线和残差图

学习曲线和残差图都是用于评估和诊断机器学习模型性能的可视化工具，是机器学习中非常重要的工具之一。

1. 学习曲线：

   学习曲线显示了模型在不同训练集大小下的表现。这可以帮助我们了解模型在增加训练样本时的性能变化。学习曲线主要包含两条曲线：训练得分曲线和交叉验证得分曲线。

   • 训练得分曲线：显示了模型在训练集上的得分（如均方误差）。当训练样本较少时，模型很容易拟合这些数据，此时训练误差较低。随着训练样本的增加，模型可能难以拟合所有数据，因此训练误差可能会上升。
   • 交叉验证得分曲线：显示了模型在交叉验证集上的得分。当训练样本较少时，模型可能过拟合，导致在交叉验证集上的性能较差。随着训练样本的增加，模型的泛化能力可能会提高，因此交叉验证误差可能会降低。

   通过观察学习曲线，我们可以诊断模型是否过拟合或欠拟合。如果训练误差和交叉验证误差之间的差距较大，说明模型可能过拟合；如果两者的误差都较高且相差不大，说明模型可能欠拟合。

2. 残差图：

   残差图显示了模型预测值与实际值之间的差距（残差）。在残差图中，横坐标表示真实值，纵坐标表示残差（预测值与真实值之差）。理想情况下，残差应该随机分布在横坐标周围，没有明显的模式。

   通过观察残差图，我们可以诊断模型是否存在系统偏差或异方差（非恒定方差）。如果残差图显示出明显的模式（如曲线或扇形），则表明模型可能无法捕捉到某些潜在的关系。在这种情况下，我们可能需要尝试使用更复杂的模型或对数据进行预处理。

SAG算法与岭回归的关系

回归问题的概念：回归问题是指根据一组自变量（特征）预测一个连续因变量（目标）的问题。线性回归是一种简单的回归模型，它试图通过拟合一个线性方程来建立输入特征与目标变量之间的关系。

SAG（随机平均梯度下降）算法是一种用于求解线性模型（如线性回归）的优化算法。它是随机梯度下降（SGD）算法的变体，但在每次迭代时，它会考虑前面所有迭代的梯度平均值。这使得SAG算法收敛得更快，同时仍然保持了SGD算法的随机性。

岭回归（Ridge Regression）是线性回归模型的一个变体，它通过在损失函数中添加一个L2正则化项来限制模型的复杂度。这有助于降低模型的过拟合风险，提高模型在新数据上的泛化能力。岭回归的求解可以通过多种优化算法实现，如梯度下降、随机梯度下降、SAG等。

SAG算法和岭回归之间的关系是：SAG算法是一种求解（包括岭回归在内的）线性模型的优化方法，而岭回归是线性回归的一种正则化变体。

提高预测准确度的方法

1. 特征工程：对特征进行筛选、变换、组合等操作，以提取更有用的信息。这可能包括去除无关特征、创建新特征、使用降维方法（如PCA）等。
2. 数据预处理：对数据进行预处理，如填充缺失值、处理异常值、数据标准化等。这有助于提高模型的泛化能力。
3. 超参数调优：通过调整模型的超参数（如学习率、正则化系数等），找到最优的参数配置。可以使用网格搜索（Grid Search）、随机搜索（Random Search）或贝叶斯优化（Bayesian Optimization）等方法进行自动调优。
4. 模型选择：尝试不同的机器学习算法，例如SVM、决策树、随机森林、神经网络等，根据具体问题选择最适合的模型。
5. 集成学习：通过集成多个模型的预测结果，提高预测的准确性。这可以包括Bagging（如随机森林）、Boosting（如AdaBoost、XGBoost）和Stacking等方法。
6. 交叉验证：使用交叉验证（如k折交叉验证）进行模型评估，以获得更稳定的性能指标。这有助于避免过拟合和欠拟合，提高模型在新数据上的表现。
7. 增加训练数据：如果可能的话，增加训练数据的数量。更多的训练数据通常会提高模型的泛化能力。
8. 数据增强：对训练数据进行扩充，增加模型的泛化能力。在图像、文本和语音等领域中，数据增强技术已被广泛应用。
9. 早停法（Early Stopping）：在训练神经网络时，通过监控验证集的性能来提前终止训练，防止模型过拟合。

人工智能的终极目标

人工智能（AI）的终极目标是创建能够模拟、理解和扩展人类智能的计算机系统。具体来说，这包括：

1. 让计算机具有学习能力，从而自动地从数据中学习规律和知识；
2. 使计算机能够理解和处理自然语言，实现与人类的自然交流；
3. 让计算机具有视觉感知能力，能够识别图像和视频中的物体、场景和动作；
4. 使计算机能够进行高级推理和决策，解决复杂问题；
5. 让计算机具有创造力，能够生成新的艺术作品、设计方案等；
6. 使计算机能够与现实世界互动，例如在机器人技术中实现感知、操作和移动等。